Learning Objectives: Define conditional and unconditional default probabilities and explain the distinction between the two. Define and use the hazard rate to calculate unconditional default probability of a credit asset.
Questions:
24.10.1. According to the 2018 Annual Global Corporate Default and Rating Transition Study, the unconditional probability that a bond will default during the fifth year is 2.38%. If the probability that it will default during the fifth year, conditional on no earlier default, is calculated to be 2.80%, what does this indicate about the nature of conditional probabilities?
a. Conditional probabilities are always higher because they account for survival until the specified condition.
b. Conditional probabilities are lower as they factor in the occurrence of defaults in earlier periods.
c. Conditional probabilities specifically reflect the likelihood of an event given that another has not occurred, making them potentially higher.
d. There is no consistent relationship; the probabilities are calculated based on different data sets.
24.10.2. Assume a firm is rated B, and based on historical data, the cumulative default probability over five years is known to be 17.33%. Calculate the average hazard rate over five years and then determine the unconditional probability of default for the sixth year, given that the hazard rate is constant.
a. 3.81% per year; Unconditional probability of 3.09% during the sixth year.
b. 3.81% per year; Unconditional probability of 3.21% during the sixth year.
c. 3.81% per year; Unconditional probability of 20.47% during the sixth year.
d. 4.07% per year; Unconditional probability of 4.39% during the sixth year.
24.10.3. An analyst at a credit rating agency is tasked with evaluating the default risk of a corporation. The analyst uses the following details:
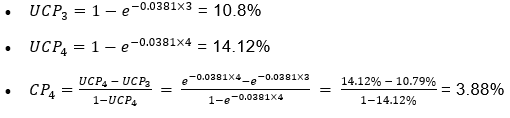
Based on this hazard rate, the analyst attempts to calculate the:
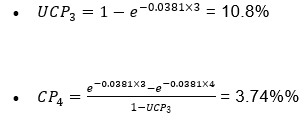
Review the analyst's calculations. Are they correct? If not, identify the errors and provide the correct calculations for UCP_3 and CP_4.
a. Both calculations are correct.
b. The calculation for UCP_3 is incorrect; UCP_3 should be calculated using a different formula.
c. The calculation for CP_4 is incorrect; CP_4 should consider the survival probability up to the end of the third year.
d. Both calculations are incorrect; the correct values for UCP_3 and CP_4 are significantly different.
Answers here:
Questions:
24.10.1. According to the 2018 Annual Global Corporate Default and Rating Transition Study, the unconditional probability that a bond will default during the fifth year is 2.38%. If the probability that it will default during the fifth year, conditional on no earlier default, is calculated to be 2.80%, what does this indicate about the nature of conditional probabilities?
a. Conditional probabilities are always higher because they account for survival until the specified condition.
b. Conditional probabilities are lower as they factor in the occurrence of defaults in earlier periods.
c. Conditional probabilities specifically reflect the likelihood of an event given that another has not occurred, making them potentially higher.
d. There is no consistent relationship; the probabilities are calculated based on different data sets.
24.10.2. Assume a firm is rated B, and based on historical data, the cumulative default probability over five years is known to be 17.33%. Calculate the average hazard rate over five years and then determine the unconditional probability of default for the sixth year, given that the hazard rate is constant.
a. 3.81% per year; Unconditional probability of 3.09% during the sixth year.
b. 3.81% per year; Unconditional probability of 3.21% during the sixth year.
c. 3.81% per year; Unconditional probability of 20.47% during the sixth year.
d. 4.07% per year; Unconditional probability of 4.39% during the sixth year.
24.10.3. An analyst at a credit rating agency is tasked with evaluating the default risk of a corporation. The analyst uses the following details:
- The corporation is initially rated B.
- The cumulative default probability over five years is noted as 17.33%.
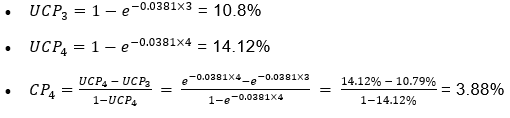
Based on this hazard rate, the analyst attempts to calculate the:
- Unconditional probability of default by the end of the third year, UCP_3.
- Conditional probability of default in the fourth year, CP_4, given that there has been no default by the end of the third year.
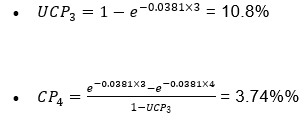
Review the analyst's calculations. Are they correct? If not, identify the errors and provide the correct calculations for UCP_3 and CP_4.
a. Both calculations are correct.
b. The calculation for UCP_3 is incorrect; UCP_3 should be calculated using a different formula.
c. The calculation for CP_4 is incorrect; CP_4 should consider the survival probability up to the end of the third year.
d. Both calculations are incorrect; the correct values for UCP_3 and CP_4 are significantly different.
Answers here:
