Learning objectives: Calculate the duration, modified duration, and dollar duration of a bond. Evaluate the limitations of duration and explain how convexity addresses some of them.
Questions
714.1. A very risky two-year bond with a face value of $100.00 pays a semi-annual coupon of 18.0% and has a yield (yield to maturity) of 15.0% with continuous compounding. Its price is therefore $104.032 as shown below. Please note that we could infer the price by translating the continuous rate into its semi-annual equivalent which is given by 2*[exp(0.150/2)-1] = 15.577% and then using the calculator: N = 4, I/Y = 15.577/2 = 7.7885%, PMT = 9, FV = 100 and CPT PV --> $104.032. The final column displays the weight of each cash flow's present value as a proportion of the bond's price.
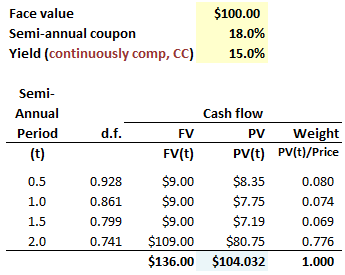
Which is nearest to the bond's duration (please note that because the yield is continuously compounded, this is the special case where Macaulay duration is equal to modified duration so we don't really need to specify which!)?
a. 1.77 years
b. 1.85 years
c. 1.93 years
d. 2.00 years
714.2. A three-year bond $1,000.00 face value bond pays a 10.0% semi-annual coupon and has a semi-annual (aka, bond equivalent) yield of 14.0%. It's price is therefore $904.67. The chart below also shows cash flows as proportional weights:
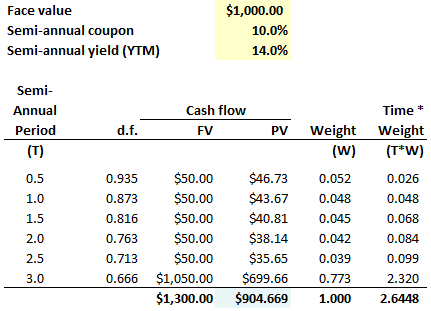
We can use modified duration to estimate the price impact of a small change in yield. Which of the following is NEAREST to a duration-based (i.e., linearly approximate) estimate of the bond's price change given a 26 basis point (0.26%) drop (shock down) to the yield?
a. $5.81
b. $6.00
c. $6.18
d. $7.25
714.3. Consider a three-year $100.00 face value bond that pays a 14.0% semi-annual coupon and offers a yield of 9.0% per annum with continuous compounding. The bond's cash flows and its duration and convexity are illustrated below. Please note the discount factors assume the yield's continuous compounding; for example, df(1.5) = exp(-0.090*1.5) = 0.87372 ≈ 0.874.
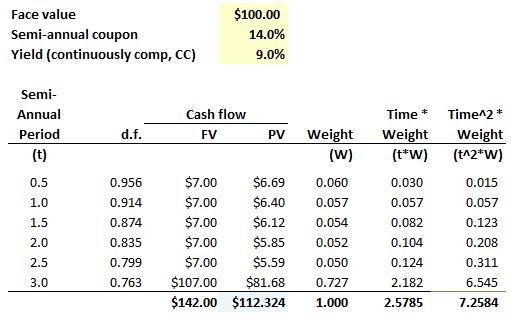
About this bond, each of the following statements is true EXCEPT which is false?
a. If the yield decreases, then (ceteris paribus) the convexity increases
b. If the yield decreases, then (ceteris paribus) then duration increases
c. If the coupon decreases, then (ceteris paribus) then the convexity decreases
d. If the yield shock is 50 basis points (0.50%), the convexity adjustment is about $0.010
Answers here:
Questions
714.1. A very risky two-year bond with a face value of $100.00 pays a semi-annual coupon of 18.0% and has a yield (yield to maturity) of 15.0% with continuous compounding. Its price is therefore $104.032 as shown below. Please note that we could infer the price by translating the continuous rate into its semi-annual equivalent which is given by 2*[exp(0.150/2)-1] = 15.577% and then using the calculator: N = 4, I/Y = 15.577/2 = 7.7885%, PMT = 9, FV = 100 and CPT PV --> $104.032. The final column displays the weight of each cash flow's present value as a proportion of the bond's price.

Which is nearest to the bond's duration (please note that because the yield is continuously compounded, this is the special case where Macaulay duration is equal to modified duration so we don't really need to specify which!)?
a. 1.77 years
b. 1.85 years
c. 1.93 years
d. 2.00 years
714.2. A three-year bond $1,000.00 face value bond pays a 10.0% semi-annual coupon and has a semi-annual (aka, bond equivalent) yield of 14.0%. It's price is therefore $904.67. The chart below also shows cash flows as proportional weights:

We can use modified duration to estimate the price impact of a small change in yield. Which of the following is NEAREST to a duration-based (i.e., linearly approximate) estimate of the bond's price change given a 26 basis point (0.26%) drop (shock down) to the yield?
a. $5.81
b. $6.00
c. $6.18
d. $7.25
714.3. Consider a three-year $100.00 face value bond that pays a 14.0% semi-annual coupon and offers a yield of 9.0% per annum with continuous compounding. The bond's cash flows and its duration and convexity are illustrated below. Please note the discount factors assume the yield's continuous compounding; for example, df(1.5) = exp(-0.090*1.5) = 0.87372 ≈ 0.874.

About this bond, each of the following statements is true EXCEPT which is false?
a. If the yield decreases, then (ceteris paribus) the convexity increases
b. If the yield decreases, then (ceteris paribus) then duration increases
c. If the coupon decreases, then (ceteris paribus) then the convexity decreases
d. If the yield shock is 50 basis points (0.50%), the convexity adjustment is about $0.010
Answers here:
Last edited by a moderator:
