Concept: These on-line quiz questions are not specifically linked to AIMs, but are instead based on recent sample questions. The difficulty level is a notch, or two notches, easier than bionicturtle.com's typical AIM-by-AIM question such that the intended difficulty level is nearer to an actual exam question. As these represent "easier than our usual" practice questions, they are well-suited to online simulation.
Questions:
413.1. Consider the following rating migration (aka, transition) matrix that gives the migration probabilities of corporate bonds for one-year period:
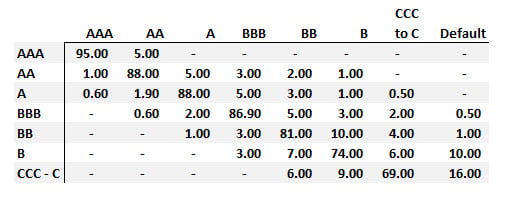
If we can assume year-to-year independence ("Markovian assumption"), which is nearest to the unconditional probability that a CCC-rated bond (the lowest rating category short of default) will default before the end of the next years?
a. 2.56%
b. 16.00%
c. 19.44%
d. 28.00%
413.2. Consider the following three-year bond with an coupon rate of 15.0% that pays an annual coupon:

Given its market price of $114.03, the bond's yield (yield to maturity) is 9.0% per annum with continuous compounding. Consequently, the one-year discount factor, df(1.0), is given by exp(-9%*1) = 0.914. Which is nearest to the modified duration of the bond?
a. 2.14 years
b. 2.65 years
c. 2.87 years
d. 3.00 years
413.3. A $1,000 face value 5-year bond that pays a 9.0% annual coupon has a Macaulay duration of 4.140 years and a modified duration of 3.600 years. If we assume an annual compound frequency (to match the annual coupon payments), which is nearest to the bond's price?
a. $798.87
b. $905.12
c. $1,138.00
d. Need more information
Answers here:
Questions:
413.1. Consider the following rating migration (aka, transition) matrix that gives the migration probabilities of corporate bonds for one-year period:

If we can assume year-to-year independence ("Markovian assumption"), which is nearest to the unconditional probability that a CCC-rated bond (the lowest rating category short of default) will default before the end of the next years?
a. 2.56%
b. 16.00%
c. 19.44%
d. 28.00%
413.2. Consider the following three-year bond with an coupon rate of 15.0% that pays an annual coupon:

Given its market price of $114.03, the bond's yield (yield to maturity) is 9.0% per annum with continuous compounding. Consequently, the one-year discount factor, df(1.0), is given by exp(-9%*1) = 0.914. Which is nearest to the modified duration of the bond?
a. 2.14 years
b. 2.65 years
c. 2.87 years
d. 3.00 years
413.3. A $1,000 face value 5-year bond that pays a 9.0% annual coupon has a Macaulay duration of 4.140 years and a modified duration of 3.600 years. If we assume an annual compound frequency (to match the annual coupon payments), which is nearest to the bond's price?
a. $798.87
b. $905.12
c. $1,138.00
d. Need more information
Answers here:
