Learning objective: Define correlation and covariance and differentiate between correlation and dependence.
Questions:
705.1. In order to evaluate the the potential of a linear relationship between portfolio returns and a benchmark index, your colleague Richard conducted a univariate regression analysis. He regressed the benchmark index returns, B(i), as the dependent (aka, response) variable against portfolio returns, R(i), as the independent (aka, explanatory) variable. Here is his summary output:
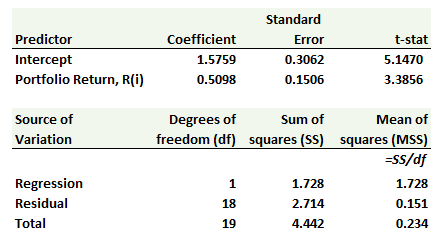
Which is nearest to the correlation coefficient between portfolio returns, R(i), and the benchmark returns, R(b)?
a. 0.4937
b. 0.5150
c. 0.6237
d. We cannot know without the adjusted R^2
705.2. Consider the following probability matrix that displays four joint probabilities, Prob(X,Y):
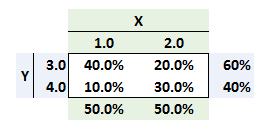
Which is nearest to the correlation between (X) and (Y)?
a. -0.35
b. Zero
c. +0.29
d. +0.41
705.3. You have assumed a single-index model and regressed the returns for two stocks, stock (A) and stock (B), against the index in separate univariate regressions. This produced the following two linear functions, such that β(A) is 0.80 and β(B) is 1.40:
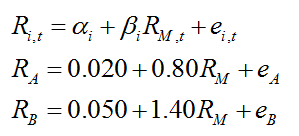
Additionally, the volatility of the index, σ(M), is 20.0%, the volatility of stock A, σ(A), is 32.0% and the volatility of stock B, σ(B), is 40.0%. Which of the following is the implied correlation between the two stocks?
a. 0.2240
b. 0.3500
c. 0.4900
d. 1.1200
Answers here:
Questions:
705.1. In order to evaluate the the potential of a linear relationship between portfolio returns and a benchmark index, your colleague Richard conducted a univariate regression analysis. He regressed the benchmark index returns, B(i), as the dependent (aka, response) variable against portfolio returns, R(i), as the independent (aka, explanatory) variable. Here is his summary output:

Which is nearest to the correlation coefficient between portfolio returns, R(i), and the benchmark returns, R(b)?
a. 0.4937
b. 0.5150
c. 0.6237
d. We cannot know without the adjusted R^2
705.2. Consider the following probability matrix that displays four joint probabilities, Prob(X,Y):

Which is nearest to the correlation between (X) and (Y)?
a. -0.35
b. Zero
c. +0.29
d. +0.41
705.3. You have assumed a single-index model and regressed the returns for two stocks, stock (A) and stock (B), against the index in separate univariate regressions. This produced the following two linear functions, such that β(A) is 0.80 and β(B) is 1.40:
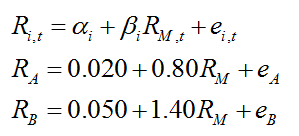
Additionally, the volatility of the index, σ(M), is 20.0%, the volatility of stock A, σ(A), is 32.0% and the volatility of stock B, σ(B), is 40.0%. Which of the following is the implied correlation between the two stocks?
a. 0.2240
b. 0.3500
c. 0.4900
d. 1.1200
Answers here:
Last edited by a moderator:
