Fran
Administrator
AIMs: Calculate the probability of an event given a discrete probability function. Distinguish between independent and mutually exclusive events. Define joint probability, describe a probability matrix and calculate joint probabilities using probability matrices.
Questions:
301.1. A random variable is given by the discrete probability function f(x) = P[X = x(i)] = a*X^3 such that x(i) is a member of {1, 2, 3} and (a) is a constant. That is, X has only three discrete outcomes. What is the probability that X will be greater than its mean? (bonus: what is the distribution's variance?)
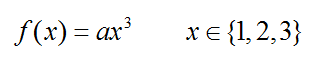
a. 45.8%
b. 50.0%
c. 62.3%
d. 75.0%
301.2. A credit asset has a principal value of $6.0 with probability of default (PD) of 3.0% and a loss given default (LGD) characterized by the following probability density function (pdf): f(x) = x/18 such that 0 ≤ x ≤ $6. Let expected loss (EL) = E[PD*LGD]. If PD and LGD are independent, what is the asset's expected loss? (note: why does independence matter?)
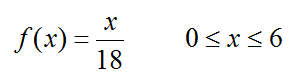
a. $0.120
b. $0.282
c. $0.606
d. $1.125
301.3. In analyzing a company, Analyst Sam prepared a probability matrix which is a joint (aka, bivariate) probability mass function that characterizes two discrete variables, equity performance versus a benchmark (over or under) and bond rating change. The company's equity performance will result in one of three mutually exclusive outcomes: under-perform, track the benchmark, or over-perform. The company's bond will either be upgraded, downgraded, or remain unchanged. Unfortunately, before Sam could share his probability matrix, he spilled coffee on it, and unfortunately some cells are not visible.
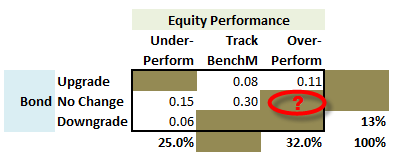
Two questions: what is the joint Prob [equity over-performs, bond has no change]; and are the two discrete variables independent?
a. 7.0%, yes
b. 12.0%, yes
c. 19.0%, no
d. 22.0%, no
Answers:
Questions:
301.1. A random variable is given by the discrete probability function f(x) = P[X = x(i)] = a*X^3 such that x(i) is a member of {1, 2, 3} and (a) is a constant. That is, X has only three discrete outcomes. What is the probability that X will be greater than its mean? (bonus: what is the distribution's variance?)
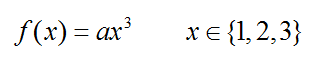
a. 45.8%
b. 50.0%
c. 62.3%
d. 75.0%
301.2. A credit asset has a principal value of $6.0 with probability of default (PD) of 3.0% and a loss given default (LGD) characterized by the following probability density function (pdf): f(x) = x/18 such that 0 ≤ x ≤ $6. Let expected loss (EL) = E[PD*LGD]. If PD and LGD are independent, what is the asset's expected loss? (note: why does independence matter?)
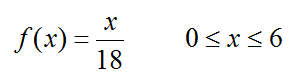
a. $0.120
b. $0.282
c. $0.606
d. $1.125
301.3. In analyzing a company, Analyst Sam prepared a probability matrix which is a joint (aka, bivariate) probability mass function that characterizes two discrete variables, equity performance versus a benchmark (over or under) and bond rating change. The company's equity performance will result in one of three mutually exclusive outcomes: under-perform, track the benchmark, or over-perform. The company's bond will either be upgraded, downgraded, or remain unchanged. Unfortunately, before Sam could share his probability matrix, he spilled coffee on it, and unfortunately some cells are not visible.

Two questions: what is the joint Prob [equity over-performs, bond has no change]; and are the two discrete variables independent?
a. 7.0%, yes
b. 12.0%, yes
c. 19.0%, no
d. 22.0%, no
Answers:

