Kavita.bhangdia
Active Member
HI David,
we have definitiions of various actives..
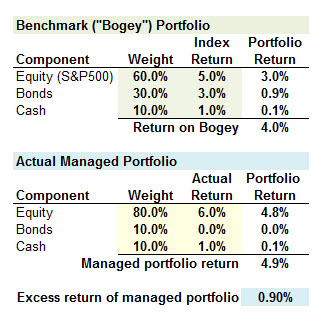
1. Active return : Portfolio return - benchmark return
2. Active risk : Standard deviation of Active risk??
3. Active weight.. No idea
Please can you help..
Thanks,
Kavita
we have definitiions of various actives..
1. Active return : Portfolio return - benchmark return
2. Active risk : Standard deviation of Active risk??
3. Active weight.. No idea
Please can you help..
Thanks,
Kavita