Variance and Covariance Calculation Clarification

[cabrown085]

Apologies in advance for any lack of precision, clearly my background is not in math.

From what I read, variance is defined as two separate formulas:

I believe I understand the first part of the equation:
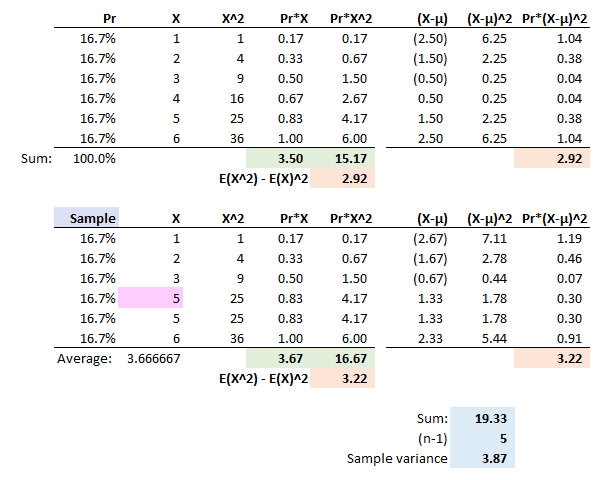
Var(X) = E[(X-u)^2]
where u = E(X):
(1) This means take the summation of: the actual values (X) MULTIPLIED by their assorted probabilities to arrive at u.
where X = is equal to each actual value.
(2) You take the series of (X - u)^2.
(3) You multiply each value of (X-u)^2 by X's assorted probability
(4) Add the total series in step 3 together.

However, Var(X) is also defined as:
Var(X)=E(X^2)-[E(X)]^2
I've been trying to wrap head around this formula:
(1) E(X^2): You take each value of X, THEN square it, and THEN multiply by the assorted probability.
(2) [E(X)]^2 I believe that this is the expected value of X (e.g., X*probability), THEN squared. Is this value the same as u and will it always be the same no matter how many Xs?
(3) You than take the difference of steps 1 and 2 for each value of X.
(4) You add the differences together to arrive at variance.

One of my questions is one of the two formulas above preferred or considered faster or more accurate?

Covariance is defined as:
Cov(X,Y)=E{[X-E(X)]*[Y-E(Y)]}

(1) E(X): Similar to above, this means take the summation of: the actual values (X) MULTIPLIED by their assorted probabilities to arrive at u or E(X). There should only be 1 E(X) value correct?
(2) E(Y): Similar to above, this means take the summation of: the actual values (Y) MULTIPLIED by their assorted probabilities to arrive at u E(Y). There should only be 1 E(Y) value correct?
(3) You add up the sum of the series of values and that gives you

Covariance is also defined as:
Cov(X,Y)=E(X,Y)-E(X)*E(Y)

Are E(X) and E(Y) the same for every instance?

Again, like my question for covariance, is one of the two formulas above preferred or considered faster or more accurate?

 

[cabrown085]

As a follow-up:

Var(X)=E(X^2)-[E(X)]^2

How does the above work with regards to this variance problem:

A discrete uniform distribution (each event has an equal probability of occurrence) has the following possible outcomes for X: [1, 2, 3, 4]. The variance of this distribution is closest to:

E(X)=2.5

Thanks!

 

[David Harper CFA FRM]

Hi @cabrown085 Let me start with the variance (as the variance is actually just a special case of the covariance, you might not have the covariance question after you grok the variance). I like to illustrate with a six-sided die. Please see the exhibit below, and here is the spreadsheet which is very simple at https://www.dropbox.com/s/9rbrctifactyljy/021716-variance.xlsx?dl=0

Your second formula, Var(X)=E(X^2)-[E(X)]^2, follows via simple mathematical proof from your first, Var(X) = E[(X-u)^2]; ie, they are mathematically equivalent.

Consider my first panel (upper) in the exhibit below. It characterizes the "true distribution" of a fair six-sided die; ie., Pr = 1/6 for each outcome. The variance of 2.92 (in orange) is calculated both ways. Personaly, I think faster is Var(X)=E(X^2)-[E(X)]^2, when it's available!

However, imagine that we don't really know the true distribution, and instead we just observe six die rolls. That is my second panel, and in this case I just imagine that we roll: 1, 2, 3, 5, 5, and 6. This is a sample, we don't expect it to perfectly match the population odds. In this case, we might implicitly assume that each outcome deserves an equal weight, in which case we could rightly compute a variance of 3.22 using either method. This is a valid variance but it assumes these six rolls represent the population, and under this assumption, again we can use either.

But it's really just a sample, so we want the sample variance, in which case I think our only approach is to sum the (X-µ)^2 and divide this by (n-1); this sample variance is 3.87 versus 3.22.

Re: discrete uniform distribution of X:[1, 2, 3 , 4], we just need the corresponding X^2:[1, 4, 9, 16]. E(X^2) = 25%*1 + 25%*4 + 25%*9 + 25%*16 = average[1,4,9,16] = 7.5, and given that E(X) = 2.5, Var(X) = 7.5 - (2.5)^2 = 1.25. Here we are treating this like a population, or put another way, we have specified the distribution as uniform discrete such that we know the 25% probabilities.

If this were a sample, then we should sum the (X-2.5)^2 = 2.25+0.25+0.25+2.25 = 5.0 and divide by (n-1) which equals 1.67 for the sample variance. Here we've assumed that we don't actually know for sure this is a discrete uniform. I hope that helps!

 

[cabrown085]

Hi David,

Thanks! I work in Excel every day so being able to look at the numbers was a big help.

What I was describing in the first part can be summed up as:
Pr*(X-µ)^2
The second equation can be described as:
Pr*X^2-(sum(Pr*X))^2.
sum(Pr*X) = µ

What you were showing in the second example was with samples it may be difficult to assign a true distribution, so instead for a sample mean, you should simply take x/n = µ
(X-µ)^2/(5)=3.87

I'm not quite sure how to drop in a table, but I follow your point with regards to covariance.