YouTube T4-43: Fixed Income: Key rate shift technique

[Nicole Seaman]

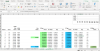
The key rate shift technique overcomes the key limitation of duration and DV01 which is that they must assume a parallel shift in the yield curve because they are single-factor risk measures. The key rate shift technique, on the other hand, is multi-factor: the term structure is carved into a limited number of "key rate regions;" in this illustration, four key rates are selected, 2-year, 5-year, 10-year, and 30-year. You can find Tuckman's Fixed Income Securities book here: https://amzn.to/2SOMGzv

 

[Bart S]

Note added by Nicole: Member is referring to a conversation within the YouTube comments and not elsewhere in the forum.

Hi David,

Let me start by reminding you of our original conversation regarding the calculation of prices with shifts in key rates:
-------------------------------------------------------
Hi David, thanks for the video, it's very clear. One question though: Since the bond only has one cash flow, that is, after 30 years, why do shifts earlier on in the curve result in a change in present value of the bond in the 2/5/10 year cases wrt the initial present value? A shift in the 30 year par yield leads to a different discount factor for the (only) cash flow, and thus in that scenario we indeed get a different present value, but if I understand it correctly, in the other cases we should find the same present value every time since we don't shock the par yields affecting the discount factor to be used for the cash flow. Hope that made sense. Thanks!

Hi Bart, yes this is easily the most challenging aspect. I followed Tuckman, as mentioned who illustrates/selects PAR YIELDS as the key rate. We do not need to choose par yields; e.g., if we use spot rates, then of course the 30-year spot rate will be unaffected by (e.g) the shift of the 10-year spot rate. But par yields are advantageous as the key rate WHEN the hedging securities are (approximately) par bonds; i.e., the hedging solution is easier. The downside to par yields (mostly) is what you are pointing out: a shift in the 10-year par yield (even as it implies no shift in the 30-year PAR YIELD per the interpolation) DOES INDEED impact the 30-year spot rate (and therefore of course the 30-year discount factor). This is counterintuitve but is explained (somewhat) in Tuckman, can be discussed further in my forum, or if you like here is my XLS where I perform the actual calculations and you can see why it must be true https://www.dropbox.com/s/1w22978jn7pkobp/071719-fixed-income-key-rates.xlsx?dl=0 Thanks,

Hi David, thanks for your reply. Is there any way you could give some more intuition about the formula used to compute the “alternative” discount factors which take into account the fact that these are par bonds? I would move this discussion to the forum if not for the fact that understanding this to me seems like a key aspect of getting the entire picture, and other viewers might be interested in this as well.

@Bart S I assume you mean: what is the intuition behind how shocking a 10-year (or 5-year) par yield, as the selected key rate, will impact the 30-year discount factor (or equivalently, the 30-year spot rate)? More generally, how can shocking an X-year par yield impact zero rates that are outside (greater than) its own region? That calculation is shows in the XLS but I can attempt an intuitive explanation by building on Tuckman's, but i'll prefer to do that in our forum and then share the link from here ... let me know if that's the right question (because the other hard question is maybe: why are par bonds better for hedging?)
-------------------------------------------------------

So indeed, I am interested in how shocking an X-year par yield can impact zero rates that are outside (greater than) its own region, and more specifically, the calculation (in your spreadsheet, for example cells K34:K92). How did you derive this formula for discount factors constructed from par yields?

But aside from that, I'm also interested in your last point, why par bonds are better for hedging.

Thanks in advance,

Best,
Bart

 

[Nicole Seaman]

Note added by Nicole: Member is referring to a conversation within the YouTube comments and not elsewhere in the forum.

Hi David,

Let me start by reminding you of our original conversation regarding the calculation of prices with shifts in key rates:
-------------------------------------------------------
Hi David, thanks for the video, it's very clear. One question though: Since the bond only has one cash flow, that is, after 30 years, why do shifts earlier on in the curve result in a change in present value of the bond in the 2/5/10 year cases wrt the initial present value? A shift in the 30 year par yield leads to a different discount factor for the (only) cash flow, and thus in that scenario we indeed get a different present value, but if I understand it correctly, in the other cases we should find the same present value every time since we don't shock the par yields affecting the discount factor to be used for the cash flow. Hope that made sense. Thanks!

Hi Bart, yes this is easily the most challenging aspect. I followed Tuckman, as mentioned who illustrates/selects PAR YIELDS as the key rate. We do not need to choose par yields; e.g., if we use spot rates, then of course the 30-year spot rate will be unaffected by (e.g) the shift of the 10-year spot rate. But par yields are advantageous as the key rate WHEN the hedging securities are (approximately) par bonds; i.e., the hedging solution is easier. The downside to par yields (mostly) is what you are pointing out: a shift in the 10-year par yield (even as it implies no shift in the 30-year PAR YIELD per the interpolation) DOES INDEED impact the 30-year spot rate (and therefore of course the 30-year discount factor). This is counterintuitve but is explained (somewhat) in Tuckman, can be discussed further in my forum, or if you like here is my XLS where I perform the actual calculations and you can see why it must be true https://www.dropbox.com/s/1w22978jn7pkobp/071719-fixed-income-key-rates.xlsx?dl=0 Thanks,

Hi David, thanks for your reply. Is there any way you could give some more intuition about the formula used to compute the “alternative” discount factors which take into account the fact that these are par bonds? I would move this discussion to the forum if not for the fact that understanding this to me seems like a key aspect of getting the entire picture, and other viewers might be interested in this as well.

@Bart S I assume you mean: what is the intuition behind how shocking a 10-year (or 5-year) par yield, as the selected key rate, will impact the 30-year discount factor (or equivalently, the 30-year spot rate)? More generally, how can shocking an X-year par yield impact zero rates that are outside (greater than) its own region? That calculation is shows in the XLS but I can attempt an intuitive explanation by building on Tuckman's, but i'll prefer to do that in our forum and then share the link from here ... let me know if that's the right question (because the other hard question is maybe: why are par bonds better for hedging?)
-------------------------------------------------------

So indeed, I am interested in how shocking an X-year par yield can impact zero rates that are outside (greater than) its own region, and more specifically, the calculation (in your spreadsheet, for example cells K34:K92). How did you derive this formula for discount factors constructed from par yields?

But aside from that, I'm also interested in your last point, why par bonds are better for hedging.

Thanks in advance,

Best,
Bart

@Bart S

Please notice that I moved your post to this thread, which is where this specific video should be discussed. It took me some time to figure out that the conversation you were referring to was on YouTube and not in the forum. Each YouTube video has a forum thread here in this section. The forum thread is located within the YouTube description so you can easily click on it and it will bring you directly to the thread for that specific video. Please make sure to post questions under the appropriate thread instead of posting a new thread. This saves us time so we are not searching for the video that you are referring to.

Thank you for being so thorough and copying the conversation that you already had with David, as this helps other members out also.

Thank you,

Nicole

 

[Bart S]

Hi David, any chance you could have a look at my question? Thanks!

 

[Matthew Graves]

I think we should first separate the two issues at play here:
1 - Deriving the zero curve
2 - Determining PV01/KRD values for a non-curve instrument

Firstly, zero rate curves are derived from observable market prices/yields and these are almost always coupon bearing instruments. The resulting zero curve will re-price the constituent instruments back to their observable market prices. If you shift, for example, the 10 year input yield then this will have an affect on the entire derived zero curve. Why? This is because all the other input yields/prices are being kept static and thus to re-price these other instrument (e.g. the 30 year) back to the observed price other rates in the zero curve will need to be reduced (slightly) to compensate for the increased 10 year yield.

So, if we now take this curve and use it to calculate PV01 or KRDs for a 30 year zero coupon bond which is not part of the observed market yields, we find that the implied 30 year zero rate (and hence the discount factor) is changed by shifting the 10 year input yield (or indeed any other input yield). This leads to non-zero PV01s for par yield shifts at maturities other than 30 years.

 

[jfeldt]

Hi David,
Please forgive this possibly quite naive question.
For a single bond, which yield curve should be used? A flat curve based on this bonds YTM?
This seems to be the most widespread usage in the examples I have seen.
Would it make sense to use the US Treasury yield curve?

Regards,
Casper

 

[Matthew Graves]

Hi David,
Please forgive this possibly quite naive question.
For a single bond, which yield curve should be used? A flat curve based on this bonds YTM?
This seems to be the most widespread usage in the examples I have seen.
Would it make sense to use the US Treasury yield curve?

Regards,
Casper

The YTM is generally just used as a measure of quoted price or value. Some bonds quote in the market using YTM, some with actual price. You are correct that the derivation or usage of YTM implies a flat curve at the YTM. YTM and Modified Duration form a sort of self-consistent simplistic universe which the literature over emphasises in my opinion.

When it comes to valuation or sensitivity analysis and a more sophisticated approach is needed, generally the corresponding government curve is used for discounting. If the bond being valued is a government bond then that is all that is required unless it is floating and you need a forecasting curve as well or use a curve consisting of floating bonds only.

For corporate (or credit risky) bonds the situation is a bit more complicated. Generally speaking though, the corresponding government curve would still be used for discounting leaving a spread above this curve to account for the credit riskiness. There's tonnes of spread measures out there including ones which account for any optionality (see Option Adjusted Spread).

 

[jfeldt]

The YTM is generally just used as a measure of quoted price or value. Some bonds quote in the market using YTM, some with actual price. You are correct that the derivation or usage of YTM implies a flat curve at the YTM. YTM and Modified Duration form a sort of self-consistent simplistic universe which the literature over emphasises in my opinion.

When it comes to valuation or sensitivity analysis and a more sophisticated approach is needed, generally the corresponding government curve is used for discounting. If the bond being valued is a government bond then that is all that is required unless it is floating and you need a forecasting curve as well or use a curve consisting of floating bonds only.

For corporate (or credit risky) bonds the situation is a bit more complicated. Generally speaking though, the corresponding government curve would still be used for discounting leaving a spread above this curve to account for the credit riskiness. There's tonnes of spread measures out there including ones which account for any optionality (see Option Adjusted Spread).

Thank you, I am somewhat familiar with the various spread measures.
I am however struggling a bit with how to use e.g. the US treasury curve when calculating key rate durations. The sum of key rates for a given security is supposed to converge to the same securitys modified/effective maturity - for which the government curve is not used, if for example a Model Evaluated Prices is available.
Your insight is appreciated.

 

[Matthew Graves]

You are correct that the sum of Key Rate Durations should be approximately equal to the Effective Duration. As with all of the these valuation type exercises, consistency is key. In all of the models I've ever seen the KRD and Effective Duration estimation procedure is essentially the same with Effective Duration involving a parallel shift of the market observed yields and KRDs a shift in the individual market yield. Thus, both of these processes will use the same input curve, whatever that is decided to be.

You may need to describe your effective duration estimation procedure for me to be of further assistance.

 

[jfeldt]

Right, I calculate a yield-based modified duration based off of the model evaluated price (from S&P), which for me then would indicate a similar approach for the key rate durations?

 

[Matthew Graves]

The yield-modified duration world is the simplest, text book situation. Calculating KRDs in this flat curve YTM world is not really done or useful. If you REALLY wanted to do this then you could make a flat curve with the YTM at each tenor point and shift each one in turn before repricing. The sum of your KRDs in that scenario should be roughly equal to the modified duration.

 

[jfeldt]

Point taken, I'll adjust.
Thank you.

 

[msoler96]

Hi David,
I have the same question as the one discussed in the Youtube thread. Where does the formula of cells K34:K92 come from? I have looked at other threads and also at Tuckman's book but I do not know how to derive the formula.
Best, Marc

 

[David Harper CFA FRM]

Hi Marc (@msoler96), Yes, let's see if i can retrieve how I did that. The key rate model is solving for the discount factor as a function of the previous discount factors and the par yield. Recall the definition of a par yield: is it the coupon rate that prices the bond (aka, PV) exactly to par. Following tuckman, the coupons are semi-annual such that the par yield relationship is given by:

1.0 = (c/2)*A + 1.0*d(T) where A is the PV of a $1.00 annuity but A does include the final coupon, just as 1.0*d(T) is only the final principal and excludes the final coupon. That is, the final coupon is located in the annuity, A.

i.e.., A = d(0.5) + d(1.0) + d(1.5) ... d(T); A is the sum of the discount factors in the discount function

So:
1.0 = (c/2)*A + 1.0*d(T)
1.0 = (c/2)*[d(0.5) + d(1.0) + ... d(T-1) + d(T)] + 1.0*d(T)
now let A(-1) = d(0.5) + d(1.0) + ... d(T-1); i.e., excluding the d(T) because we need to solve for d(T), so A(-1) is the truncated annuity if you will.

1.0 = (c/2)*[A(-1) + d(T)] + 1.0*d(T)
1.0 = (c/2)*A(-1) + (c/2)*d(T) + 1.0*d(T)
1.0 - (c/2)*A(-1) = (c/2)*d(T) + 1.0*d(T)
1.0 - (c/2)*A(-1) = [(c/2) + 1.0]*d(T), multiply both sides by 2:
2.0 - c*A(-1) = [c + 2.0]*d(T), and finally solving for d(T):
[2.0 - c*A(-1)]/(c + 2.0) = d(T)

... of course, once done, it is trivial to confirm (in the XLS with dynamic variables) that it works.

I hope that helps, I should add this into the XLS, thank you for asking me to do it!

 

[msoler96]

Hi David,
Thank you so much for such a quick and precise answer.
It's always a pleasure to learn from your content.
Best,
Marc

 

[nc27]

Hi @David Harper CFA FRM , I hope you and your relatives are doing well.

I was reviewing one of your learning spreadsheet about examples that are found in Tuckman (chapter about modeling and hedging non-parallel term structure shifts) and I had a doubt on how some discount factors are computed, could you help me ? I have done a screenshot of one of the example where the discount formula can be seen. Thanks

 

[David Harper CFA FRM]

Hi @nc27 Thank you for the kind wishes! I moved your question to this thread. You are asking about the discount factors that are implied by the par yield (where the par yields are shocked per key rate shift technique). You'll see above at https://forum.bionicturtle.com/threads/t4-43-fixed-income-key-rate-shift-technique.22781/post-83413 how the discount factor is retrieved by solving-for d(T) given the definition of the par yield; ie,

1.0 = (c/2)*A + 1.0*d(T) where A is the PV of a $1.00 annuity but A does include the final coupon, just as 1.0*d(T) is only the final principal and excludes the final coupon. That is, the final coupon is located in the annuity, A.

i.e.., A = d(0.5) + d(1.0) + d(1.5) ... d(T); A is the sum of the discount factors in the discount function

So:
1.0 = (c/2)*A + 1.0*d(T)
1.0 = (c/2)*[d(0.5) + d(1.0) + ... d(T-1) + d(T)] + 1.0*d(T)
now let A(-1) = d(0.5) + d(1.0) + ... d(T-1); i.e., excluding the d(T) because we need to solve for d(T), so A(-1) is the truncated annuity if you will.

1.0 = (c/2)*[A(-1) + d(T)] + 1.0*d(T)
1.0 = (c/2)*A(-1) + (c/2)*d(T) + 1.0*d(T)
1.0 - (c/2)*A(-1) = (c/2)*d(T) + 1.0*d(T)
1.0 - (c/2)*A(-1) = [(c/2) + 1.0]*d(T), multiply both sides by 2:
2.0 - c*A(-1) = [c + 2.0]*d(T), and finally solving for d(T):
[2.0 - c*A(-1)]/(c + 2.0) = d(T)

I hope that's helpful,

 

[nc27]

Thank you David!

 

[Susanna3890]

Hallo all, can someone help me to solve this? I do not understand how we can use linear interpolation to solve this problem...
-Text:
Assume par yield KR01s are calculated using five-and ten-year shifts in par yields. A portfolio has an exposure
KR01 (Five-Year Shift) KR01 (Ten-Year Shift) of +50 to a one-basis-point change in the seven-year par yield. Use linear interpolation to determine its par yield KR01s