gargi.adhikari
Active Member
Hi,
In reference to:
R31.P1.T4- Tuckman Chapter 2-Learning SpreadsheetT4.c Bundle : Sheet-Maturity vs Price
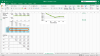
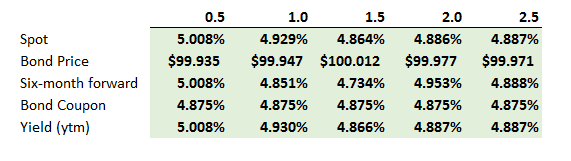
Please refer to the section circled in orange in the screenshot below. The Coupon is = 4.875% based on which the Cash Flows have been derived. But to calculate the discounted Prices for this bond, we have used the discount factors for another bond which has a different set of Coupons (highlighted in yellow) from which the discount factors have been deduced. How are we using discount factors for one bond for another bond...? I am probably missing a point or two here... Any insights on this would be much appreciated !
Any insights on this would be much appreciated ! 

In reference to:
R31.P1.T4- Tuckman Chapter 2-Learning SpreadsheetT4.c Bundle : Sheet-Maturity vs Price
Please refer to the section circled in orange in the screenshot below. The Coupon is = 4.875% based on which the Cash Flows have been derived. But to calculate the discounted Prices for this bond, we have used the discount factors for another bond which has a different set of Coupons (highlighted in yellow) from which the discount factors have been deduced. How are we using discount factors for one bond for another bond...? I am probably missing a point or two here...
 Any insights on this would be much appreciated !
Any insights on this would be much appreciated !