Learning objectives: Describe performance manipulation and the problems associated with using conventional performance measures. Describe techniques to measure the market timing ability of fund managers with a regression and with a call option model and compute return due to market timing. Describe and apply performance attribution procedures, including the asset allocation decision, sector and security selection decision, and the aggregate contribution.
Questions:
21.12.1. Bodie, Kane and Marcus explain, based on an analogy originally developed by Robert C. Merton, that we can attempt to quantify the value of market timing by recognizing that foresight is similar to holding a call option on the owned equity portfolio (without paying the premium): the perfect market timer exercises her option, so to speak, by switching from the riskfree asset to the equity portfolio (or vice-versa) depending on which offers the better return. Consequently, the Black-Scholes (BSM) formula can be used, but when the strike price is given by $1.00*exp(r*T), the BSM call option formula conveniently reduces to c = 2*N[0.5*σ(e)*sqrt(T)]-1.
If we assume annual forecasts (T = 1.0 year), and the volatility of the equity portfolio, σ(e) = 36.0% per annum, which of the following is nearest to the value of perfect market timing, as a percentage of the equity portfolio's value?
a. 7.39%
b. 14.28%
c. 46.50%
d. 83.77%
21.12.2. Patty is an analyst who makes a bull-or-bear forecast each quarter. Let's consider her timing ability over the last two years (eight quarters). The actual market was a bull (i.e., positive excess returns) for the first six (6) quarters, then slumped into a bear (i.e., negative excess returns) for the final two (2) quarters.
Patty was a bull for the first five (5) quarters, then she turned bearish for the remaining three (3) quarters. In this way, she was only one quarter early in her switch from bull to bear. Which of the following is nearest to her market timing score?
a. 0.375
b. 0.833
c. 1.000
d. 1.667
21.12.3. The scatterplot below graphs a portfolio's excess returns (Y-axis) against the market index's excess return (X-axis) for the last 12 months. Per Treynor and Mazuy's regression test of timing ability, the portfolio's excess returns, Rp, were regressed against the market index's excess return, Rm, plus this return squared, Rm^2. Therefore, the regression takes the form given by Rp = α + β*Rm + c*Rm^2 + ε. The resultant coefficients are alpha, α = 0.76, β = 1.37, and c = 0.20. Their respective standard errors, which are displayed below the coefficients, are se(α) = 0.607, se(β) = 0.169, and se(c) = 0.042.
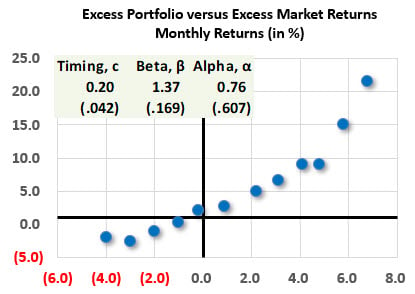
Our confidence level is (two-sided) is 95.0%. Is there statistical evidence of stock selection skill, systematic exposure (i.e., beta with respect to the market index) and/or market timing ability?
a. The portfolio has significantly negative beta with market timing success and evident stock selection skill
b. The portfolio has significantly positive beta and evident stock selection skill, but there is no evidence of market timing success
c. The portfolio has significantly positive beta with market timing success, and perhaps stock selection skill but this is unclear
d. The portfolio has neither significant beta nor evident market timing success, but there is evident stock selection skill
Answers here:
Questions:
21.12.1. Bodie, Kane and Marcus explain, based on an analogy originally developed by Robert C. Merton, that we can attempt to quantify the value of market timing by recognizing that foresight is similar to holding a call option on the owned equity portfolio (without paying the premium): the perfect market timer exercises her option, so to speak, by switching from the riskfree asset to the equity portfolio (or vice-versa) depending on which offers the better return. Consequently, the Black-Scholes (BSM) formula can be used, but when the strike price is given by $1.00*exp(r*T), the BSM call option formula conveniently reduces to c = 2*N[0.5*σ(e)*sqrt(T)]-1.
If we assume annual forecasts (T = 1.0 year), and the volatility of the equity portfolio, σ(e) = 36.0% per annum, which of the following is nearest to the value of perfect market timing, as a percentage of the equity portfolio's value?
a. 7.39%
b. 14.28%
c. 46.50%
d. 83.77%
21.12.2. Patty is an analyst who makes a bull-or-bear forecast each quarter. Let's consider her timing ability over the last two years (eight quarters). The actual market was a bull (i.e., positive excess returns) for the first six (6) quarters, then slumped into a bear (i.e., negative excess returns) for the final two (2) quarters.
Patty was a bull for the first five (5) quarters, then she turned bearish for the remaining three (3) quarters. In this way, she was only one quarter early in her switch from bull to bear. Which of the following is nearest to her market timing score?
a. 0.375
b. 0.833
c. 1.000
d. 1.667
21.12.3. The scatterplot below graphs a portfolio's excess returns (Y-axis) against the market index's excess return (X-axis) for the last 12 months. Per Treynor and Mazuy's regression test of timing ability, the portfolio's excess returns, Rp, were regressed against the market index's excess return, Rm, plus this return squared, Rm^2. Therefore, the regression takes the form given by Rp = α + β*Rm + c*Rm^2 + ε. The resultant coefficients are alpha, α = 0.76, β = 1.37, and c = 0.20. Their respective standard errors, which are displayed below the coefficients, are se(α) = 0.607, se(β) = 0.169, and se(c) = 0.042.

Our confidence level is (two-sided) is 95.0%. Is there statistical evidence of stock selection skill, systematic exposure (i.e., beta with respect to the market index) and/or market timing ability?
a. The portfolio has significantly negative beta with market timing success and evident stock selection skill
b. The portfolio has significantly positive beta and evident stock selection skill, but there is no evidence of market timing success
c. The portfolio has significantly positive beta with market timing success, and perhaps stock selection skill but this is unclear
d. The portfolio has neither significant beta nor evident market timing success, but there is evident stock selection skill
Answers here:
Last edited by a moderator:
