gargi.adhikari
Active Member
In reference to P1.T4.VAR-HULL-
Ch15_LearningSpreadsheet_4b.3.volatility_ma:
I was trying to work out the Std Dev formula:
SQRT[ sum( squared x) / (n-1) - { (sum(x) ^ 2 ) / n*(n-1) } ]
which is :-
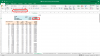
=SQRT(I4/(n-1)-F4^2/(n*(n-1))) in the sheet below.
= SQRT [ .1603/ (120-1) - {(20.13/100 ) ^ 2 } / 120* (120-1) ] --> but this is not yielding the 2.9840% ...am getting a different no plugging in all the values...
When I had used the traditional Std Dev formula : SQRT[ sum{( x-avg)^ 2} / (n-1) ], I had gotten the 2.984 % value....but plugging in the values into the other formula am not getting the same value as indicated in the Learning Spreadsheet...what am I missing here ... ??????
??????
Ch15_LearningSpreadsheet_4b.3.volatility_ma:
I was trying to work out the Std Dev formula:
SQRT[ sum( squared x) / (n-1) - { (sum(x) ^ 2 ) / n*(n-1) } ]
which is :-
=SQRT(I4/(n-1)-F4^2/(n*(n-1))) in the sheet below.
= SQRT [ .1603/ (120-1) - {(20.13/100 ) ^ 2 } / 120* (120-1) ] --> but this is not yielding the 2.9840% ...am getting a different no plugging in all the values...
When I had used the traditional Std Dev formula : SQRT[ sum{( x-avg)^ 2} / (n-1) ], I had gotten the 2.984 % value....but plugging in the values into the other formula am not getting the same value as indicated in the Learning Spreadsheet...what am I missing here ...
 ??????
??????

 and thanks for taking the time for the clarification. Yes when I plugged the 10.63% , the variation of the std-dev formula yielded the expected value of 2.984%. I do prefer to use the formula Σ[u(i)^2]/(n-1) - [Σu(i)]^2/[n*(n-1)] for the std - dev and so wanted to make sure I was doing it right. Thanks again !
and thanks for taking the time for the clarification. Yes when I plugged the 10.63% , the variation of the std-dev formula yielded the expected value of 2.984%. I do prefer to use the formula Σ[u(i)^2]/(n-1) - [Σu(i)]^2/[n*(n-1)] for the std - dev and so wanted to make sure I was doing it right. Thanks again !