AIMs: Identify the components of a U.S. Treasury coupon bond, and compare and contrast the structure to Treasury STRIPS, including the difference between P-STRIPS and C-STRIPS. Construct a replicating portfolio using multiple fixed income securities to match the cash flows of a given fixed income security. Identify arbitrage opportunities for fixed income securities with certain cash flows.
Questions:
310.1. The first three US Treasury bonds listed below are the "base bonds:" they inform the market's efficient discount function up to 1.5 years, with semi-annual compounding:
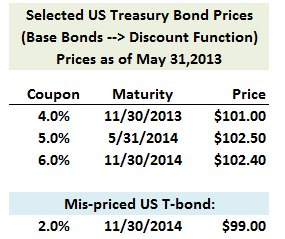
We also observe a 1.5 year Treasury bond (matures on 11/30/2014) with a 2.0% coupon that is mis-priced at $99.00. If we use the three base bonds to replicate a portfolio with identical cash flows (i.e., identical to the mis-priced 2.0% bond), in order to exploit the arbitrage opportunity (assume no transaction costs), what is the trade with respect to the base 6.0% 11/30/2014 bond?
a. Sell 0.9320 face amount of the 6.0% 11/30/14 T-bond for a receipt of $95.33
b. Sell 1.0472 face amount of the 6.0% 11/30/14 T-bond for a receipt of $113.20
c. Buy 0.9806 face amount of the 6.0% 11/30/14 T-bond at a cost of $100.41
d. Buy 0.9740 face amount of the 6.0% 11/30/14 T-bond at a cost of $96.43
310.2. Assume we observe the prices of Treasury coupon STRIPS, C-STRIPS:
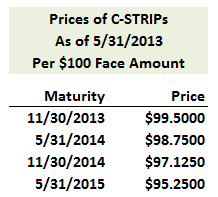
Based on these C-STRIP prices, which of the following is nearest to the computed (model) price of a two-year 4.0% coupon bond that matures on 5/31/15?
a. $96.50
b. $98.1250
c. $100.750
d. $103.06250
310.3. Your colleague Robert is constructing a discount function using the market prices of Treasury STRIPS to infer the term structure of discount factors. However, he asks you to help him resolve an apparently violation of the "law of one price:" at several maturities, he observes a significant difference between the observed market price of a STRIP security and calculated price calculated (aka, model price) derived by employing the discount factors. Which of the following is the best explanation for market-versus-model price difference?
a. The Treasury STRIPS will have various coupon rates, such that the discount function is non-trivial and model-dependent
b. The market prices reflect, at certain identical maturities, both C-STRIPS and on-the-run P-STRIPS
c. The P-STRIPS are fungible but the C-STRIPS are not
d. This is a nonsensical hypothetical which is unlikely to occur in practice as arbitrage renders the law of one price highly resistant to violations
Answers:
Questions:
310.1. The first three US Treasury bonds listed below are the "base bonds:" they inform the market's efficient discount function up to 1.5 years, with semi-annual compounding:

We also observe a 1.5 year Treasury bond (matures on 11/30/2014) with a 2.0% coupon that is mis-priced at $99.00. If we use the three base bonds to replicate a portfolio with identical cash flows (i.e., identical to the mis-priced 2.0% bond), in order to exploit the arbitrage opportunity (assume no transaction costs), what is the trade with respect to the base 6.0% 11/30/2014 bond?
a. Sell 0.9320 face amount of the 6.0% 11/30/14 T-bond for a receipt of $95.33
b. Sell 1.0472 face amount of the 6.0% 11/30/14 T-bond for a receipt of $113.20
c. Buy 0.9806 face amount of the 6.0% 11/30/14 T-bond at a cost of $100.41
d. Buy 0.9740 face amount of the 6.0% 11/30/14 T-bond at a cost of $96.43
310.2. Assume we observe the prices of Treasury coupon STRIPS, C-STRIPS:

Based on these C-STRIP prices, which of the following is nearest to the computed (model) price of a two-year 4.0% coupon bond that matures on 5/31/15?
a. $96.50
b. $98.1250
c. $100.750
d. $103.06250
310.3. Your colleague Robert is constructing a discount function using the market prices of Treasury STRIPS to infer the term structure of discount factors. However, he asks you to help him resolve an apparently violation of the "law of one price:" at several maturities, he observes a significant difference between the observed market price of a STRIP security and calculated price calculated (aka, model price) derived by employing the discount factors. Which of the following is the best explanation for market-versus-model price difference?
a. The Treasury STRIPS will have various coupon rates, such that the discount function is non-trivial and model-dependent
b. The market prices reflect, at certain identical maturities, both C-STRIPS and on-the-run P-STRIPS
c. The P-STRIPS are fungible but the C-STRIPS are not
d. This is a nonsensical hypothetical which is unlikely to occur in practice as arbitrage renders the law of one price highly resistant to violations
Answers:
