AIMs: Describe spectral risk measures, and explain how VaR and ES are special cases of spectral risk measures.
Questions:
31.1. For a certain operational process, the frequency distribution below implies a 20% probability of two (2) loss events during the month. For each loss event that occurs, the severity distribution is given by: 50% probability of $1,000 loss (i.e., the loss amount conditional on a loss occurrence), 20% probability of $10,000 loss, and 10% probability of $100,000 loss:
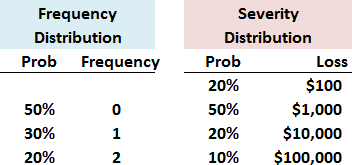
Assuming the frequency and severity are independent, what is the 99.0% monthly expected shortfall (ES) of the aggregate (tabulated) loss?
a. $110,000
b. $128,000
c. $140,000
d. $200,000
31.2. Each of the following is true about spectral risk measures EXCEPT for:
a. Both value at risk (VaR) and expected shortfall (ES) are spectral measures
b. Neither VaR nor ES are coherent
c. Expected shortfall gives all weights in the tail region an equal weight, which implies the user is risk-neutral between tail-region outcomes
d. According to Dowd, the best risk measure would reflect users' risk aversion and therefore employ a weighting function that assigns higher weights to greater losses, but neither VaR nor ES reflect this risk-aversion
31.3. The spectral risk measure is a weighted average of the quantiles of the loss distribution, as follows:
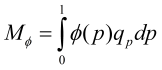
where phi(p) is the weighting function. Each of the following is TRUE about this spectral risk measure EXCEPT for:
a. In the special case of VaR, phi(p) assigns a weight of 1.0 to the event p = %confidence, and a weight of zero to p<>%confidence
b. In the special case of ES, phi(p) assigns a weight of 1/(1-%confidence) if p >= %confidence, and a weight of zero to p<%confidence
c. To reflect risk-aversion and demonstrate coherence, the optimal spectral risk measure has a weighting function, phi(p), that is weakly increasing: if p2> p1, it should be that phi(p2) > phi(p1)
d. Under equilibrium, and the assumptions of the spectral risk measure, there exists a single, "one size fits all" exponential weighting function, phi(p), that satisfies the no arbitrage bounds
Answers:
Questions:
31.1. For a certain operational process, the frequency distribution below implies a 20% probability of two (2) loss events during the month. For each loss event that occurs, the severity distribution is given by: 50% probability of $1,000 loss (i.e., the loss amount conditional on a loss occurrence), 20% probability of $10,000 loss, and 10% probability of $100,000 loss:

Assuming the frequency and severity are independent, what is the 99.0% monthly expected shortfall (ES) of the aggregate (tabulated) loss?
a. $110,000
b. $128,000
c. $140,000
d. $200,000
31.2. Each of the following is true about spectral risk measures EXCEPT for:
a. Both value at risk (VaR) and expected shortfall (ES) are spectral measures
b. Neither VaR nor ES are coherent
c. Expected shortfall gives all weights in the tail region an equal weight, which implies the user is risk-neutral between tail-region outcomes
d. According to Dowd, the best risk measure would reflect users' risk aversion and therefore employ a weighting function that assigns higher weights to greater losses, but neither VaR nor ES reflect this risk-aversion
31.3. The spectral risk measure is a weighted average of the quantiles of the loss distribution, as follows:
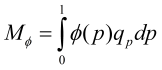
where phi(p) is the weighting function. Each of the following is TRUE about this spectral risk measure EXCEPT for:
a. In the special case of VaR, phi(p) assigns a weight of 1.0 to the event p = %confidence, and a weight of zero to p<>%confidence
b. In the special case of ES, phi(p) assigns a weight of 1/(1-%confidence) if p >= %confidence, and a weight of zero to p<%confidence
c. To reflect risk-aversion and demonstrate coherence, the optimal spectral risk measure has a weighting function, phi(p), that is weakly increasing: if p2> p1, it should be that phi(p2) > phi(p1)
d. Under equilibrium, and the assumptions of the spectral risk measure, there exists a single, "one size fits all" exponential weighting function, phi(p), that satisfies the no arbitrage bounds
Answers:
