Questions:
324.1. Consider the following GARCH(1,1) model:
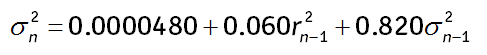
Each of the following is true about this GARCH(1,1) model EXCEPT which is false?
a. If the volatility(n-1) is 5.0% and the return(n-1) is 3.0%, then the updated volatility estimate is about 4.6390%
b. The 10-day forward forecast (n+10) is a daily volatility of about 2.980%
c. The model's long-run (unconditional) volatility is 3.3%
d. The model's persistence is 0.880
324.2. Analyst Barbara employs an exponentially weighted moving average (EWMA) volatility model to generate a current daily volatility estimate of 2.15%. This EWMA model updates yesterday's volatility of 2.0% with yesterday's daily return of +3.0%. Which is nearest to her lambda parameter?
a. 0.79340
b. 0.87550
c. 0.91810
d. 0.95430
324.3 Consider the historical series of stock prices below, including the daily returns and the squared daily returns (Return^2). Although only the previous nine days are displayed, the actual horizon includes 55 trading days. The volatility estimates computed for the previous day, t-1, are given for each of the GARCH(1,1), EWMA and moving average (MA) methods. Also given are the lambda for the EWMA model and the GARCH parameters; e.g., the unconditional long-run variance, V(L), is 3.0%^2; the gamma weight applied to this long-run variance is 10%, such that omega = 10%*3.0%^2 = 0.000090:
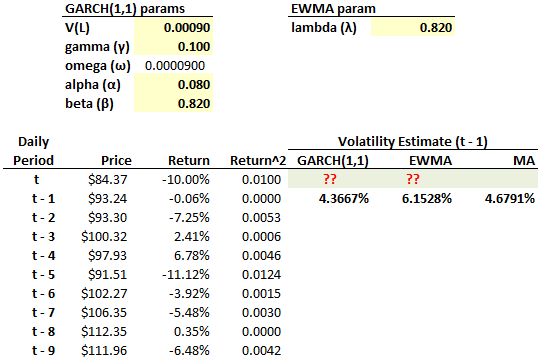
Today's price drop contributes a dramatic -10.00% return to the series! Which are nearest to the updated volatility estimates given by, respectively, GARCH(1,1) and EWMA? Bonus question: what are the WEIGHTS assigned by each of these models to the (t-5) return^2; i.e., the fifth previous return was also dramatic at -11.12%, what weight is assigned to its square, under each method?
a. GARCH = 4.73% and EWMA = 4.90%
b. GARCH = 4.95% and EWMA = 7.00%
c. GARCH = 5.25 % and EWMA = 5.25%
d. GARCH = 5.25% and EWMA = 5.74%
Answers:
324.1. Consider the following GARCH(1,1) model:
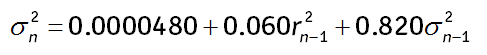
Each of the following is true about this GARCH(1,1) model EXCEPT which is false?
a. If the volatility(n-1) is 5.0% and the return(n-1) is 3.0%, then the updated volatility estimate is about 4.6390%
b. The 10-day forward forecast (n+10) is a daily volatility of about 2.980%
c. The model's long-run (unconditional) volatility is 3.3%
d. The model's persistence is 0.880
324.2. Analyst Barbara employs an exponentially weighted moving average (EWMA) volatility model to generate a current daily volatility estimate of 2.15%. This EWMA model updates yesterday's volatility of 2.0% with yesterday's daily return of +3.0%. Which is nearest to her lambda parameter?
a. 0.79340
b. 0.87550
c. 0.91810
d. 0.95430
324.3 Consider the historical series of stock prices below, including the daily returns and the squared daily returns (Return^2). Although only the previous nine days are displayed, the actual horizon includes 55 trading days. The volatility estimates computed for the previous day, t-1, are given for each of the GARCH(1,1), EWMA and moving average (MA) methods. Also given are the lambda for the EWMA model and the GARCH parameters; e.g., the unconditional long-run variance, V(L), is 3.0%^2; the gamma weight applied to this long-run variance is 10%, such that omega = 10%*3.0%^2 = 0.000090:

Today's price drop contributes a dramatic -10.00% return to the series! Which are nearest to the updated volatility estimates given by, respectively, GARCH(1,1) and EWMA? Bonus question: what are the WEIGHTS assigned by each of these models to the (t-5) return^2; i.e., the fifth previous return was also dramatic at -11.12%, what weight is assigned to its square, under each method?
a. GARCH = 4.73% and EWMA = 4.90%
b. GARCH = 4.95% and EWMA = 7.00%
c. GARCH = 5.25 % and EWMA = 5.25%
d. GARCH = 5.25% and EWMA = 5.74%
Answers:
