Questions:
316.1. Assume a 99.0% daily value at risk (VaR) model is perfectly accurate. Specifically, among 100 days, we expect a loss that exceeds VaR on exactly one day. The probability mass function of a binomial distribution is given by:
.png)
Over a series of 20 trading days, which is nearest to the probability that the daily loss will exceed VaR on exactly two (2) days?
a. 0.44%
b. 0.93%
c. 1.59%
d. 2.36%
316.2. The frequency of "Damage to Physical Assets," an operational risk event type, is characterized by a Poisson distribution. Over an average year, a company expects 36 of these particular loss events. During the next month, which is nearest to the probability the company will experience exactly zero (none) of these events?
a. 3.4%
b. 5.0%
c. 7.5%
d. 9.1%
316.3. The current price of an asset is S(0) and its future evolution is modeled with a binomial tree. At each node, there is a 62% probability of an (jump-up) increase. If the price increases, the next price is given by S(T+1)=S(T)*1.050; if the price decreases, the next price is given by S(T+1)=S(T)/1.050. Over the next year, there are twelve time steps, one for each month. Which is nearest to the probability that the final price of the asset is exactly the same as its current current price, S(0)?
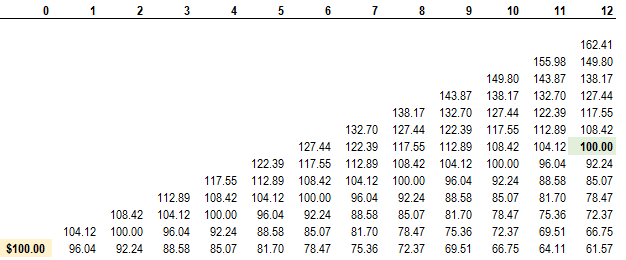
a. 15.80%
b. 19.33%
c. 22.25%
d. 33.67%
Answers:
316.1. Assume a 99.0% daily value at risk (VaR) model is perfectly accurate. Specifically, among 100 days, we expect a loss that exceeds VaR on exactly one day. The probability mass function of a binomial distribution is given by:
.png)
Over a series of 20 trading days, which is nearest to the probability that the daily loss will exceed VaR on exactly two (2) days?
a. 0.44%
b. 0.93%
c. 1.59%
d. 2.36%
316.2. The frequency of "Damage to Physical Assets," an operational risk event type, is characterized by a Poisson distribution. Over an average year, a company expects 36 of these particular loss events. During the next month, which is nearest to the probability the company will experience exactly zero (none) of these events?
a. 3.4%
b. 5.0%
c. 7.5%
d. 9.1%
316.3. The current price of an asset is S(0) and its future evolution is modeled with a binomial tree. At each node, there is a 62% probability of an (jump-up) increase. If the price increases, the next price is given by S(T+1)=S(T)*1.050; if the price decreases, the next price is given by S(T+1)=S(T)/1.050. Over the next year, there are twelve time steps, one for each month. Which is nearest to the probability that the final price of the asset is exactly the same as its current current price, S(0)?

a. 15.80%
b. 19.33%
c. 22.25%
d. 33.67%
Answers:
