Fran
Administrator
AIM: Define, calculate, and interpret the covariance and correlation between two random variables.
Questions:
304.1. Two assets, X and Y, produce only three joint outcomes: Prob[X = -3.0%, Y = -2.0%] = 30%, Prob[X = +1.0%, Y = +2.0%] = 50%, and Prob[X = +5.0%, Y = +3.0%] = 20%:
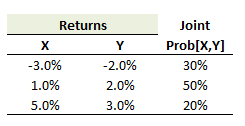
What is the correlation between X & Y? (bonus question: if we removed the probabilities and instead simply treated the three sets of returns as a small [tiny actually!] historical sample, would the sample correlation be different?)
a. 0.6330
b. 0.7044
c. 0.8175
d. 0.9286
304.2. Each of random variable X and Y can have two outcomes. The following probability matrix gives their joint probabilities:
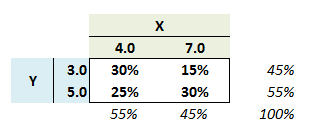
For example, the joint Prob[X = 4.0, Y = 3.0] = 30%. What is the covariance between X and Y?
a. -0.9727
b. 0.3150
c. 1.4842
d. 4.9224
304.3. Let X be a discrete uniform random integer in the set {1, 2, 3, 4, 5} with equal probability of each outcome and let Y = (X+1)^2:
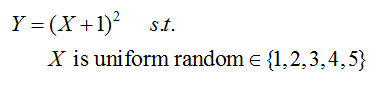
What is the covariance between X & Y?
a. 5.5
b. 9.0
c. 16.0
d. 25.0
Answers:
Questions:
304.1. Two assets, X and Y, produce only three joint outcomes: Prob[X = -3.0%, Y = -2.0%] = 30%, Prob[X = +1.0%, Y = +2.0%] = 50%, and Prob[X = +5.0%, Y = +3.0%] = 20%:

What is the correlation between X & Y? (bonus question: if we removed the probabilities and instead simply treated the three sets of returns as a small [tiny actually!] historical sample, would the sample correlation be different?)
a. 0.6330
b. 0.7044
c. 0.8175
d. 0.9286
304.2. Each of random variable X and Y can have two outcomes. The following probability matrix gives their joint probabilities:

For example, the joint Prob[X = 4.0, Y = 3.0] = 30%. What is the covariance between X and Y?
a. -0.9727
b. 0.3150
c. 1.4842
d. 4.9224
304.3. Let X be a discrete uniform random integer in the set {1, 2, 3, 4, 5} with equal probability of each outcome and let Y = (X+1)^2:
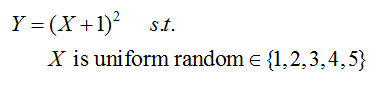
What is the covariance between X & Y?
a. 5.5
b. 9.0
c. 16.0
d. 25.0
Answers:
