Learning objectives: Calculate, distinguish and convert between simple and continuously compounded returns. Define and distinguish between volatility, variance rate, and implied volatility. Describe how the first two moments may be insufficient to describe non-normal distributions.
Questions:
21.3.1. A concentrated fund has only four positions. At the beginning of the week, its initial value was $1,000. The daily log returns for the portfolio over the five-day trading week are displayed in the upper panel below; these log returns are suspiciously round for the sake of simple calculations but please assume they are accurate daily log returns. In the lower panel, the corresponding simple (aka, discrete holding period) returns are given; for example, on Monday the first (Asset #1) asset's log return was 2.00% which corresponds to exp(2%)-1 = 2.020134% but this is rounded in display to 2.020%.
With respect to this portfolio, four associates at the firm (Alice, Bob, Casandra, and Donald) make the following four assertions:
a. Only Alice and Donald are correct
b. Only Bob and Casandra are correct
c. None of them are correct
d. All four of them are correct
21.3.2. Jack wants to estimate the volatility of a stock based on its daily closing prices last week. He realizes this is a very small sample. The prices, along with the implied simple and log returns, are displayed below.

In the final two columns, the daily returns have been squared (and the sum of those squared returns are shown at the bottom). Because the sample is small, Jack computes his volatility based on an unbiased sample variance. Further, although he realizes that variance is the average squared difference from the mean, for purpose of this calculation he will assume the mean daily return is zero (please note there is indeed good theoretical justification for "excluding" the mean from the variance calculation for purposes of the volatility estimate); put simply, he will not be using the average daily returns displayed on the bottom row as this simplifies his calculation. Finally, although he realizes he can use either return, for this purpose he prefers the log returns because they are time-additive.
Which is nearest to Jack's daily volatility calculation based on log returns, assuming zero mean and an unbiased sample variance?
a. 5.33%
b. 6.50%
c. 9.67%
d. 13.00%
21.3.3. To estimate the risk of a stock, Peter calculates the daily sample standard deviation based on historical daily log returns (n = 250) over the last year. Based on his calculations over this historical sample, the daily volatility was 1.60%. Using this 1.60% as an input, Peter performs two calculations to produce a value at risk (VaR) estimate.
a. Alice
b. Bob
c. Cindy
d. Earl
Answers here:
Questions:
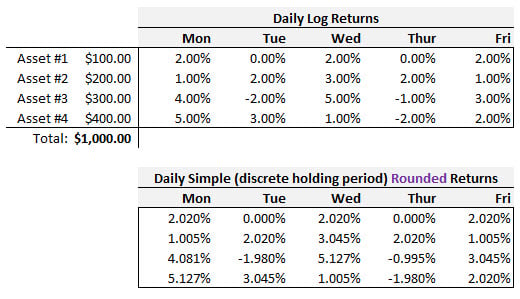
21.3.1. A concentrated fund has only four positions. At the beginning of the week, its initial value was $1,000. The daily log returns for the portfolio over the five-day trading week are displayed in the upper panel below; these log returns are suspiciously round for the sake of simple calculations but please assume they are accurate daily log returns. In the lower panel, the corresponding simple (aka, discrete holding period) returns are given; for example, on Monday the first (Asset #1) asset's log return was 2.00% which corresponds to exp(2%)-1 = 2.020134% but this is rounded in display to 2.020%.

With respect to this portfolio, four associates at the firm (Alice, Bob, Casandra, and Donald) make the following four assertions:
- Alice says Asset #3 had a 5-day log return of exactly +9.0% because an asset's weekly log return is the sum of its daily log returns; that is, she observes that 4.0% -2.0% +5.0% -1.0% +3.0% = +9.0%.
- Bob says Asset #3 had a 5-day holding period (aka, simple) return of 9.42% because an asset's weekly simple return is the sum of its daily simple returns; that is, he observes that 4.018% - 1.980% + ... + 3.045% = + 9.278% where exp(4.0%)-1 = 4.018%.
- Casandra says that the portfolio's log return on Monday was exactly 3.60% because the portfolio's daily log return is the weighted average of its components log returns; that is, she observes that (10%*2.0%) + (20%*1.0%) + (30%*4.0%) + (40%*5.0%) = 3.60%.
- Donald says that the portfolio's holding period (aka, simple) return on Monday was 3.6782% because the portfolio's daily simple return is the weighted average of its components simple returns; that is, he observes that (10%*2.020%) + (20%*1.005%) + (30%*4.081%) + (40%*5.127%) = 3.67818% exp(2.0%)-1 = 2.02%.
a. Only Alice and Donald are correct
b. Only Bob and Casandra are correct
c. None of them are correct
d. All four of them are correct
21.3.2. Jack wants to estimate the volatility of a stock based on its daily closing prices last week. He realizes this is a very small sample. The prices, along with the implied simple and log returns, are displayed below.

In the final two columns, the daily returns have been squared (and the sum of those squared returns are shown at the bottom). Because the sample is small, Jack computes his volatility based on an unbiased sample variance. Further, although he realizes that variance is the average squared difference from the mean, for purpose of this calculation he will assume the mean daily return is zero (please note there is indeed good theoretical justification for "excluding" the mean from the variance calculation for purposes of the volatility estimate); put simply, he will not be using the average daily returns displayed on the bottom row as this simplifies his calculation. Finally, although he realizes he can use either return, for this purpose he prefers the log returns because they are time-additive.
Which is nearest to Jack's daily volatility calculation based on log returns, assuming zero mean and an unbiased sample variance?
a. 5.33%
b. 6.50%
c. 9.67%
d. 13.00%
21.3.3. To estimate the risk of a stock, Peter calculates the daily sample standard deviation based on historical daily log returns (n = 250) over the last year. Based on his calculations over this historical sample, the daily volatility was 1.60%. Using this 1.60% as an input, Peter performs two calculations to produce a value at risk (VaR) estimate.
- First, he scales the daily volatility to an annual volatility per 1.60% * sqrt(250) = 25.30%, and thusly determines that the stock's volatility is 25.30% per annum.
- Second, he multiplies the annualized volatility by a quantile (aka, deviate) of 1.645 per 25.30% * 1.645 = 41.62%, and concludes that 41.62% is the relative value at risk (VaR) in percentage terms.
- Alice says that his method is correct under any and all assumptions
- Bob says that his first step imposes (aka, requires) normality and his second step requires independence (the i.i.d. assumption)
- Cindy says that his first step requires independence (the i.i.d. assumption) and his second step imposes (aka, requires) normality
- Earl says actual returns tend to skewed, heavy-tailed, and positively autocorrelated such that Peter's estimate is higher than (aka, overstates) the true 95.0% one-year relative VaR.
a. Alice
b. Bob
c. Cindy
d. Earl
Answers here:
Last edited by a moderator:
