Learning objectives: Define and describe the properties of autoregressive (AR) processes. Define and describe the properties of moving average (MA) processes. Explain how a lag operator works.
Questions:
20.22.1. Below are a set of innovations over ten steps (from initial t = 0 to t = 10) and the first innovation ε(1) = 0.26. The innovations are random Gaussian white noise, ε(t) ~ N(0, σ^2 = 1).
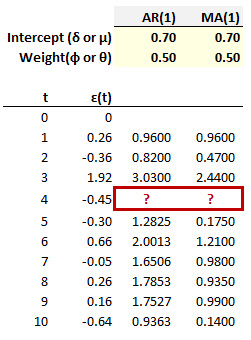
Consider two time series models. The AR(1) model has an intercept, δ, of 0.70, and an AR parameter, ϕ, of 0.50. As an AR(1) model is specified by Y(t) = ẟ + ϕ*Y(t-1) + ε(t), this AR(1) model is therefore given by Y(t) = 0.70 + 0.50*Y(t-1) + ε(t). The MA(1) model has a mean, μ, of 0.70, and a weight of 0.50. As an MA(1) model is specified by Y(t) = μ + θ*ε(t-1) + ε(t), this MA(1) is therefore given by Y(t) = 0.70 + 0.50*ε(t-1) + ε(t). Which of the following is nearest the value at t = 4; i.e., which are the missing values inside the red rectangle?
a. AR(1) = 1.7650 and MR(1) = 1.2100
b. AR(1) = 1.9630 and MR(1) = 1.8550
c. AR(1) = 2.8600 and MR(1) = 2.2570
d. AR(1) = 3.2430 and MR(1) = 2.6800
20.22.2. The following code simulates an autoregressive (AR) processes and a moving average (MA) process. The key argument is order=c(p, d, q): p is the AR order (i.e., the number of autoregressive terms), d is the number of nonseasonal differences, and q is the MA order. The "n = 200" argument specifies the length of the simulation. The MA(1) simulation is achieved with c(0, 0, 1) and the AR(1) simulation is achieved with c(1, 0, 0). In both processes, the random shock is white noise: e(t) ~ WN(0, 1) with unit variance.

Below is a plot of the two simulations:
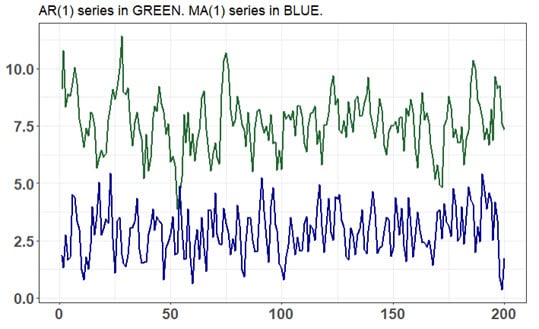
About these AR(1) and MA(1) simulations, each of the following statements is true EXCEPT which is false?
a. The MA(1) process has a mean of 2.0
b. The AR(1) process has a long-run (aka, unconditional) mean of 7.50
c. Both of these AR(1) and MA(1) processes are covariance-stationary
d. Both the these AR(1) and MA(1) processes have unconditional variances of 1.0
20.22.3. Consider the following four time series models that employ a lag operator:
I. Y(t) = (1 + 0.30L)*ε(t)
II. (1 - 0.40L)*Y(t) = 1.50 + ε(t)
III. (1 - 0.50L)*Y(t) = 3.80 + (1 + 0.74L)*ε(t)
IV. ϕ(L)*Y(t) = 3.80 + θ(L)*ε(t)
Please assume here that "mean" refers to the unconditional mean of the time series. Which of the following accurately describes (in sequence) the four models above (I. to IV.)?
a. I. ARMA, II. ARMA(1,1) with mean of 6.0, III. AR(2) with mean of 3.80, and IV. MA(p,q)
b. I. MA(1) with mean of zero, II. AR(1) with mean of 2.50, III. ARMA(1,1) with mean of 7.60, and IV. ARMA
c. I. AR(1) with mean of 0.30, II. MA(1) with mean of 1.50, III. ARMA(1,1) with mean of zero, and IV. ARMA
d. I. MA(2) with mean of zero, II. AR(2) with mean of 1.50, III. ARMA(2,2) with mean of 3.80, and IV. ARMA
Answers here:
Questions:
20.22.1. Below are a set of innovations over ten steps (from initial t = 0 to t = 10) and the first innovation ε(1) = 0.26. The innovations are random Gaussian white noise, ε(t) ~ N(0, σ^2 = 1).

Consider two time series models. The AR(1) model has an intercept, δ, of 0.70, and an AR parameter, ϕ, of 0.50. As an AR(1) model is specified by Y(t) = ẟ + ϕ*Y(t-1) + ε(t), this AR(1) model is therefore given by Y(t) = 0.70 + 0.50*Y(t-1) + ε(t). The MA(1) model has a mean, μ, of 0.70, and a weight of 0.50. As an MA(1) model is specified by Y(t) = μ + θ*ε(t-1) + ε(t), this MA(1) is therefore given by Y(t) = 0.70 + 0.50*ε(t-1) + ε(t). Which of the following is nearest the value at t = 4; i.e., which are the missing values inside the red rectangle?
a. AR(1) = 1.7650 and MR(1) = 1.2100
b. AR(1) = 1.9630 and MR(1) = 1.8550
c. AR(1) = 2.8600 and MR(1) = 2.2570
d. AR(1) = 3.2430 and MR(1) = 2.6800
20.22.2. The following code simulates an autoregressive (AR) processes and a moving average (MA) process. The key argument is order=c(p, d, q): p is the AR order (i.e., the number of autoregressive terms), d is the number of nonseasonal differences, and q is the MA order. The "n = 200" argument specifies the length of the simulation. The MA(1) simulation is achieved with c(0, 0, 1) and the AR(1) simulation is achieved with c(1, 0, 0). In both processes, the random shock is white noise: e(t) ~ WN(0, 1) with unit variance.

Below is a plot of the two simulations:

About these AR(1) and MA(1) simulations, each of the following statements is true EXCEPT which is false?
a. The MA(1) process has a mean of 2.0
b. The AR(1) process has a long-run (aka, unconditional) mean of 7.50
c. Both of these AR(1) and MA(1) processes are covariance-stationary
d. Both the these AR(1) and MA(1) processes have unconditional variances of 1.0
20.22.3. Consider the following four time series models that employ a lag operator:
I. Y(t) = (1 + 0.30L)*ε(t)
II. (1 - 0.40L)*Y(t) = 1.50 + ε(t)
III. (1 - 0.50L)*Y(t) = 3.80 + (1 + 0.74L)*ε(t)
IV. ϕ(L)*Y(t) = 3.80 + θ(L)*ε(t)
Please assume here that "mean" refers to the unconditional mean of the time series. Which of the following accurately describes (in sequence) the four models above (I. to IV.)?
a. I. ARMA, II. ARMA(1,1) with mean of 6.0, III. AR(2) with mean of 3.80, and IV. MA(p,q)
b. I. MA(1) with mean of zero, II. AR(1) with mean of 2.50, III. ARMA(1,1) with mean of 7.60, and IV. ARMA
c. I. AR(1) with mean of 0.30, II. MA(1) with mean of 1.50, III. ARMA(1,1) with mean of zero, and IV. ARMA
d. I. MA(2) with mean of zero, II. AR(2) with mean of 1.50, III. ARMA(2,2) with mean of 3.80, and IV. ARMA
Answers here:
Last edited by a moderator:
