P1 T1 Quantitative analysis (Miller ch2)

[Hesham_87]

Dear David,

while studying Miller ch2, I just wanna ask several questions:

based on definition of Joint Probability “The joint probability distribution of two discrete random variables, say X and Y, is the probability that the random variables simultaneously take on certain values, say x and y. The probabilities of all possible (x, y) combinations sum to 1. The joint probability distribution can be written as the function Pr(X = x, Y = y).” — Stock & Watson"

1- is it correct to consider that all joint probabilities are independent events?

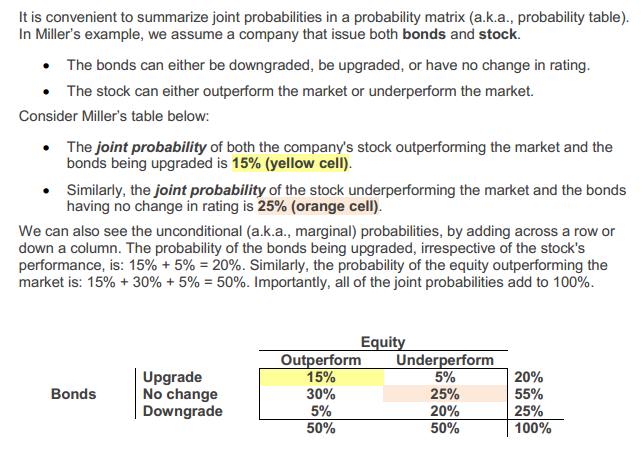
2- Page number 11 in Miller chapter 2 study note, the example of bonds and equity, it is understood that the probability of upgrading bond AND probability of outperform the stock is 15%, my question why did we add the following events ( probability of upgrading bonds, probability of outperforming stock AND probability of under performing stock) to get 20%, i mean it does not make sense a stock to outperform and under perform @ the same time, right?

 

[David Harper CFA FRM]

Hi @Hesham_87 Sure thing! I copied a snapshot below. This happens to be our render of Miller's Probability Matrix (Exhibit 2.3). There is more than one way to represent a probability distribution, but this is a helpful way, I think. The nature of a Probability Matrix, which is necessarily a discrete probability mass function, includes:

• Each of the joint outcomes (a cell inside the matrix; e.g., 15% probability of jointly bond upgrade and equity outperforms) is a probability
• Each of the joint probabilities is mutually exclusive: in any given single trial, only one of the outcomes is possible. As you suggest, it is not possible for simultaneously the equity to both outperform and under-perform. It is not possible for simultaneously a bond to upgrade and downgrade. (These simple models are single-period. None of this means to suggest the bond can't upgrade this period then downgrade next period. Hence my use of "simultaneous").
• Because the probability matrix is a (discrete) probability distribution, the cells inside the square must sum to 100%. (so, too, the outside row and columns, which represent unconditional distributions, as opposed to inside cells which are joint distributions)

Then to your questions:

1. Are the cells (ie, the joint probabilities) independent? No, not necessarily. But maybe. We require them to mutually exclusive, but not independent. Independence implies that the bond's outcome is unrelated (has no effect on) the equity's outcome. It is tested with: does unconditional Pr[Bond event]*unconditional Pr[equity event] = joint Pr[Bond event, equity event]. Notice, for example, that Pr[Bond upgrade]*Pr[equity outperform] = 20%*50% = 10% but this is not equal to their joint probability of 15%. All we need is to find one exception. Since we did, we find that these cells are not independent.
2. Adding the 15% and 5% is taking advantage of their mutual exclusivity in order to determine the unconditional probability of a bond upgrade. This is an "or" that is connecting them, not an "and;" ie.., what is the (unconditional) probability that the bond upgrades? It can upgrade while equity outperforms or while equity underperforms. Miller actually anticipates this potential confusion:

"MUTUALLY EXCLUSIVE EVENTS > For a given random variable, the probability of any of two mutually exclusive events occurring is just the sum of their individual probabilities. In statistics notation, we can write:
(2.12) P(A∪B) = P(A)+P(B)
where is the union of A and B. This is the probability of either A or B occurring. This is true only of mutually exclusive events. This is a very simple rule, but, as mentioned at the beginning of the chapter, probability can be deceptively simple, and this property is easy to confuse. The confusion stems from the fact that and is synonymous with addition. If you say it this way, then the probability that A or B occurs is equal to the probability of A and the probability of B. It is not terribly difficult, but you can see where this could lead to a mistake. This property of mutually exclusive events can be extended to any number of events. The probability that any of n mutually exclusive events occurs is simply the sum of the probabilities of those n events." -- Miller, Michael B.. Mathematics and Statistics for Financial Risk Management (Wiley Finance) (Kindle Locations 759-771). Wiley. Kindle Edition.

I hope that clarifies!

 

[Hesham_87]

Thank You