Meissner's chapter-1: Correlation Basics

[charyaua]

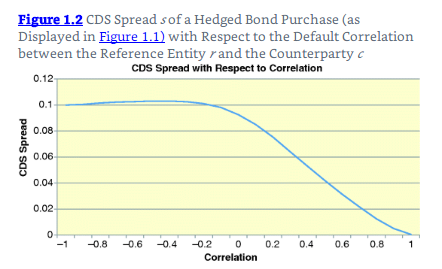
In the Meissner's chapter-1: Correlation Basics, there is a graph that shows the relationship between Correlation and Spread.

"we observe that for a correlation of -0.30 and higher, the higher the correlation, the lower the CDS spread. This is because an increasing r means a higher probability of the reference asset and the counterparty defaulting together."


Should not the spread be higher when correlation is higher owing to the increased risk? If it is, why is that spread is lower in this case?

Secondly, does correlation higher than 0 (positive side) mean that the CDS issuer (BNP Paribas) and the Sovereign country (Spain) debt, don't default together. As the graph indicates, above 0 correlations seems to bring the spread down. Why is that?

 

[David Harper CFA FRM]

Hi @charyaua

That's a good graph to focus on (reproduced below for reference). This is confusing because a bond and a CDS have different superficial dynamics. Keep in mind that, if you buy (i.e., long position) a bond, you would hedge the default risk by purchasing a credit default swap (ie,, long CDS which is short the reference bond). Keeping it real simple, assume the riskfree rate (eg US Treasury) is 2.0% and you buy a (risky) bond with a 5.0% yield; then you hedge by purchasing a CDS with a premium of 3.0% (ie, 5% received - 3% paid = 2% which should put you roughly in a risk-free position, ignoring several nuances). Now, let's say the risky bond experiences a credit deterioration or downgrade. With respect to the bond, its price goes down and its yield goes up. With respect to the CDS, its value goes up (ie, PV of either leg) and its premium (the CDS spread) goes up. Maybe the bond's price drops and its yield increases from 5.0% to 6.0%; the CDS spread should increase to 4.0%. Greater risk --> higher spread. So far so good, but this ignores counterparty risk.

The analogy to the CDS premium payments is insurance premiums. In the graph below, as correlation tends toward 1.0, if you are the protection buyer, you are looking at a situation where you are less likely to receive your "insurance settlement" (i.e., the contingent payoff in the event of default) if the bond defaults, because the bond and the counterparty are more likely to default together. Under these conditions (which, analogously to your worry that the insurance company might be going out of business or doesn't actually have capital to settle your claim), you are willing to pay less premium. This is the counterparty risk. While an increase in default probability of the underlying bond will increase the spread (and value) of the CDS, due to increased risk, wrong-way risk (greater default correlation with the counterparty) has the opposite effect, it lowers the CDS buyer's premium. I hope that clarifies!

 

[charyaua]

Yes it does and it could not be more clear and crisp.

Thanks David