Roshan Ramdas
Active Member
Hi David,
Need your help with the below question please (from the BT 2010 mock). I've copied out 2 passages which have conflicting opinions about the impact of higher interest rates on MBS investors.
Passage 1 seems to suggest that investors are benefitted by prepayment at higher interest rates on account of better reinvestment income potential.
Passage 2 seems to indicate that investors do not benefit at high and low yields.
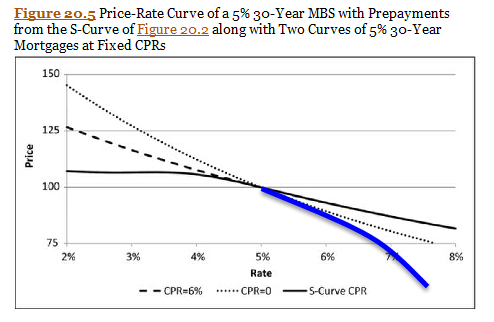
Question - How does the embedded option in the mortgage pass-through impact the price-yield curve at HIGHER yields (think of the answer to 8.2)?
Passage 1 (from the mock pdf itself)
As Tuckman explains, “this phenomenon [higher price than noncallable equivalent at higher yields] is due to the fact that housing turnover, defaults, and disasters generate prepayments even when rates are relatively high. And when rates are high relative to the existing mortgage rate, prepayments benefit investors in the pass-through: A below-market fixed income investment is returned to these investors at par.” To summarize 8.3 and 8.4, the embedded call in the mortgage pass-through creates negative convexity at low yields (a generic feature of the embedded call) AND increases the price (relative to a nonprepayable mortgage) at higher yields (a specific feature of mortgagor dynamics).
Passage 2 (from BT question bank)
D. Negative convexity is unfavorable to the long at both low and high yields. (and so the investor is compensated with a higher yield, ceteris paribus) Fabozzi: "It is important to understand how changes in prepayment rates impact the performance of mortgages and MBS. Since prepayments increase as bond prices rise and market yields are declining, mortgages shorten in average life and duration when the bond markets rally, constraining their price appreciation. Conversely, rising yields cause prepayments to slow and bond durations to extend, resulting in a greater drop in price than experienced by more traditional (i.e., option-free) fixed income products. As a result, the price performance of mortgages and MBS tends to lag that of comparable fixed maturity instruments (such as Treasury notes) when the prevailing level of yields increases. This phenomenon is generically described as “negative convexity.” The effect of changing prepayment speeds on mortgage durations, based on movements in interest rates, is precisely the opposite of what a bondholder would desire. (Fixed income portfolio managers, for example, extend durations as rates decline, and shorten them when rates rise.) The price performance of mortgages and MBS is, therefore, decidedly nonlinear in nature, and the product will underperform assets that do not exhibit negatively convex behavior as rates decline."
Thank you
Need your help with the below question please (from the BT 2010 mock). I've copied out 2 passages which have conflicting opinions about the impact of higher interest rates on MBS investors.
Passage 1 seems to suggest that investors are benefitted by prepayment at higher interest rates on account of better reinvestment income potential.
Passage 2 seems to indicate that investors do not benefit at high and low yields.
Question - How does the embedded option in the mortgage pass-through impact the price-yield curve at HIGHER yields (think of the answer to 8.2)?
Passage 1 (from the mock pdf itself)
As Tuckman explains, “this phenomenon [higher price than noncallable equivalent at higher yields] is due to the fact that housing turnover, defaults, and disasters generate prepayments even when rates are relatively high. And when rates are high relative to the existing mortgage rate, prepayments benefit investors in the pass-through: A below-market fixed income investment is returned to these investors at par.” To summarize 8.3 and 8.4, the embedded call in the mortgage pass-through creates negative convexity at low yields (a generic feature of the embedded call) AND increases the price (relative to a nonprepayable mortgage) at higher yields (a specific feature of mortgagor dynamics).
Passage 2 (from BT question bank)
D. Negative convexity is unfavorable to the long at both low and high yields. (and so the investor is compensated with a higher yield, ceteris paribus) Fabozzi: "It is important to understand how changes in prepayment rates impact the performance of mortgages and MBS. Since prepayments increase as bond prices rise and market yields are declining, mortgages shorten in average life and duration when the bond markets rally, constraining their price appreciation. Conversely, rising yields cause prepayments to slow and bond durations to extend, resulting in a greater drop in price than experienced by more traditional (i.e., option-free) fixed income products. As a result, the price performance of mortgages and MBS tends to lag that of comparable fixed maturity instruments (such as Treasury notes) when the prevailing level of yields increases. This phenomenon is generically described as “negative convexity.” The effect of changing prepayment speeds on mortgage durations, based on movements in interest rates, is precisely the opposite of what a bondholder would desire. (Fixed income portfolio managers, for example, extend durations as rates decline, and shorten them when rates rise.) The price performance of mortgages and MBS is, therefore, decidedly nonlinear in nature, and the product will underperform assets that do not exhibit negatively convex behavior as rates decline."
Thank you