Dr. Jayanthi Sankaran
Well-Known Member
Hi David,
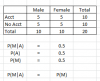
Q. A. 11. In an introductory accounting class there are 500 students, of which 300 are males and 200 are females. Of these, 100 males and 60 females plan to major in accounting. A student is selected at random from this class, and it is found that this student plans to be an accounting major. What is the probability that the student is a male?
A. A. 11. Let A denote the event that the student is male and B that the student is an accounting major. Therefore, we want to find out P(A|B). From the formula of conditional probability just given, this probability can be obtained as
P(A|B) = P(AB) = 100/500
P(B) 160/500
= 0.625
Although, this example appears to be very simple, I am confused. Does the above answer imply that events A and B are not statistically independent? Specifically I don't understand the numerator 100/500...
Thanks
Jayanthi
Q. A. 11. In an introductory accounting class there are 500 students, of which 300 are males and 200 are females. Of these, 100 males and 60 females plan to major in accounting. A student is selected at random from this class, and it is found that this student plans to be an accounting major. What is the probability that the student is a male?
A. A. 11. Let A denote the event that the student is male and B that the student is an accounting major. Therefore, we want to find out P(A|B). From the formula of conditional probability just given, this probability can be obtained as
P(A|B) = P(AB) = 100/500
P(B) 160/500
= 0.625
Although, this example appears to be very simple, I am confused. Does the above answer imply that events A and B are not statistically independent? Specifically I don't understand the numerator 100/500...
Thanks

Jayanthi