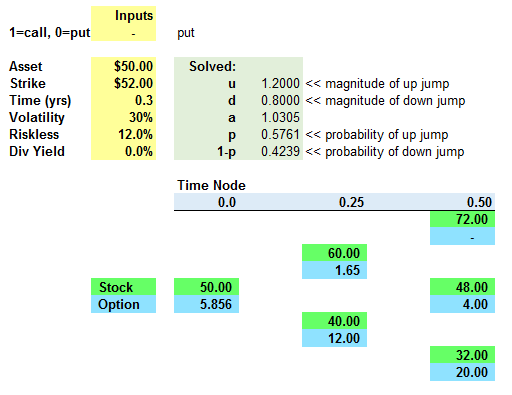
Hi @David Harper CFA FRM CIPM In question set R30.P1.T4.Hull question no.1.4(page 4) there is question like follows:

And there is also explanation of this question on page page 7 as follows:

But I think there is something missing there, when I calculated the prices as follows:
1st price=e^-4%($3.63*0.321)=$1.119541
and option price=e^-4%(1.119541*0.321)=$0.345281. That means answer needs to be a.0.35. Correct me if I am wrong.
Thank you
And there is also explanation of this question on page page 7 as follows:

But I think there is something missing there, when I calculated the prices as follows:
1st price=e^-4%($3.63*0.321)=$1.119541
and option price=e^-4%(1.119541*0.321)=$0.345281. That means answer needs to be a.0.35. Correct me if I am wrong.
Thank you