Dr. Jayanthi Sankaran
Well-Known Member
Hi David,
I have the following questions:
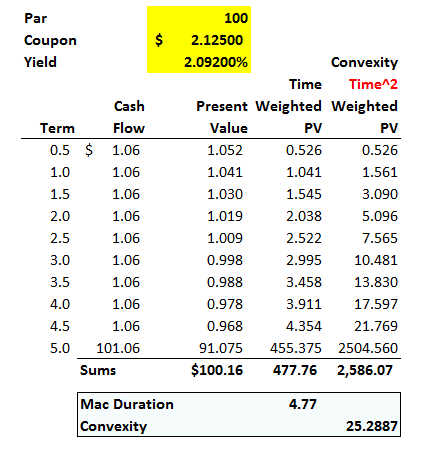
(1) Will the FRM require us to apply equation (12.49) on page 226 to data such as those on Table 12-6 pg 223 of Tuckman for yield based convexity?
(2) On time-weighting the Present Value in Table 12-6 by (t/2)*(t+1)/2, I get the convexity = 27.98 while Tuckman gets convexity = 25.29. I don't know if this is because he time weights it by t^2.
(3) On using equation (12.51) on page 226, for a five-year zero coupon bond yielding 2.092%, I get the same convexity as Tuckman = 26.93
(4) The convexity of the five year zero coupon bond = 26.93 > convexity of the five year coupon bond = 25.29 as in Tuckman. This is what one would expect.
(5) However, in my case the convexity of the five year coupon = 27.98 > convexity of the five year zero = 26.93 which is counterintuitive.
Is this because of rounding errors?
Thanks!
Jayanthi
I have the following questions:
(1) Will the FRM require us to apply equation (12.49) on page 226 to data such as those on Table 12-6 pg 223 of Tuckman for yield based convexity?
(2) On time-weighting the Present Value in Table 12-6 by (t/2)*(t+1)/2, I get the convexity = 27.98 while Tuckman gets convexity = 25.29. I don't know if this is because he time weights it by t^2.
(3) On using equation (12.51) on page 226, for a five-year zero coupon bond yielding 2.092%, I get the same convexity as Tuckman = 26.93
(4) The convexity of the five year zero coupon bond = 26.93 > convexity of the five year coupon bond = 25.29 as in Tuckman. This is what one would expect.
(5) However, in my case the convexity of the five year coupon = 27.98 > convexity of the five year zero = 26.93 which is counterintuitive.
Is this because of rounding errors?
Thanks!
Jayanthi
Last edited: